Investigación

Breviario

En la actualidad existe una gran variedad de aplicaciones –software– que requieren de protocolos de autenticación que brinden testimonio de la identidad digital de los participantes en alguna comunicación en diversos ambientes de cómputo.

Este proyecto de investigación tiene como objetivo, en el aspecto práctico, proponer un protocolo de autenticación basado en pruebas de conocimiento nulo (zero-knowledge proofs) y en la complejidad computacional del problema de conjuntos independientes en teoría de grafos y, en el aspecto teórico, estudiar familias de ciclos hamiltonianos en grafos hipercubo.

Exploramos las características de ciclos hamiltonianos en hipercubos de dimensión n, proponemos criterios de equivalencias y con ello clases, mismas que pueden tener propiedades útiles para fines criptográficos y por último, proponer un conjunto de herramientas que realicen operaciones criptográficas basados en los problemas de grafos, anteriormente descritos.

Intereses

  • Autenticación digital
  • Teoría de gráfos
  • Criptografía
  • Seguridad

Cursos

  • image

    Seminario de Doctorado 4

    Profesor: Guillermo Benito Morales Luna

    Horario:

    • el miércoles 21 de septiembre, de las 12:00 a 14:00 horas,
    • los viérnes del 5 de octubre al 20 de noviembre, de las 12:00 a 14:00 horas.

    Más detalles

Proyectos derivados

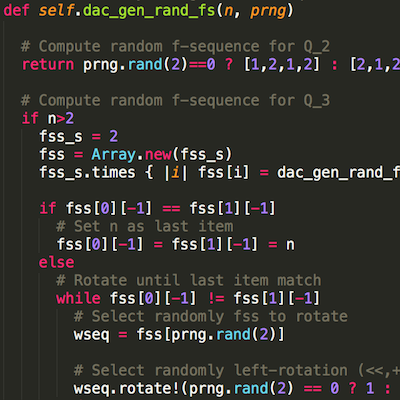
  • image

    Bibliotecas para manejo de F-secuencias

    Las f-secuencias son secuencias de números que pueden describir ciclos hamiltonianos en un hipercubo de n dimensiones, mediante los índices de las dimensiones que un ciclo debe ir recorriendo en el grafo.

    He desarrollado un par de bibliotecas para generar, usar y manipular –principalmente–f-secuencias. Una en lenguaje C y otra en Ruby, llamadas fseq4c y fseq4r, respectivamente.

    Ambas bibliotecas continúan en desarrollo y constantes modificaciones. El código es libre y se encuentra disponible para su uso. Cualquier contribución –mejora, comentarios, reporte de errores, sugerencias, etc.– es bien recibida y agradecida.

    Repositorios:

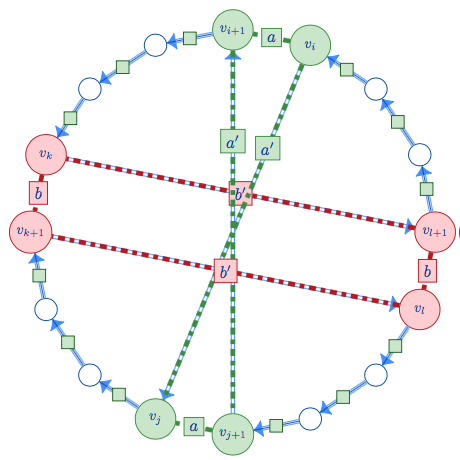
  • image

    Reporte técnico de relaciones entre clases de secuencias-f mínimas mediante la transformación trébol invertido en el hipercubo de dimensión 4

    En este documento describimos una transformación que llamamos trébol invertido. Este está basado en dos cuadros, uno recto y otro torcido. La aplicación de esta transformación da como resultado una secuencia-f mínima que no es f-equivalente a la secuencia de origen. Esto define una relación de equivalencia basada en esta transformación.

    El documento está disponible en el archivo inclfsn4.pdf en formato PDF.

    Las diferentes versiones están disponibles en su repositorio que se cita a continuación.

    Repositorio:

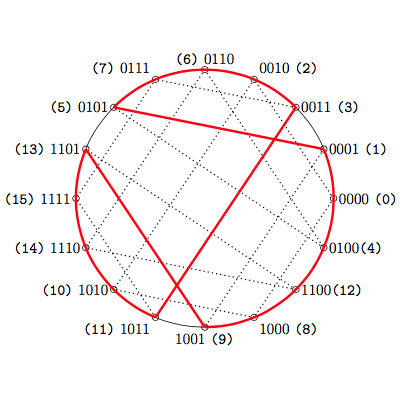
  • image

    Reporte técnico de relaciones de clases secuencias-f mediante la transformación hongo en el hipercubo de dimensión 4

    Un tema de interés en el estudio de las secuencias-f es contar cuántas clases de equivalencia existen en un hipercubo y si acaso existe relación entre las secuencias de las clases de equivalencia mediante una transformación que denominamos hongo (nombre que le dimos por su parecido con la forma de un hongo cuando se le dibuja).

    En este documento mencionamos las clases de equivalencia de las secuencias-f en el hipercubo de dimensión 4, nos referimos a cada una mediante su representante mínimo y mostramos las relaciones que hemos encontrado entre estas clases de equivalencia mediante la transformación hongo.

    El documento está disponible en el archivo mshtrnsq4rsch.pdf en formato PDF.

    Las diferentes versiones están disponibles en su repositorio que se cita a continuación.

    Repositorios:

  • image

    Reporte técnico de “Programas generadores de secuencias-f”

    En este trabajo exploramos una alternativa para representar secuencias-f basada en programas que las generan. Estos programas están basados en la definición de operaciones para estas secuencias y mediante la composición de estos programas generar otras.

    Las secuencias-f de orden n representan familias de ciclos hamiltonianos en el hipercubo de n dimensiones, por lo tanto, su representación como una secuencia de índices de coordenadas de su espacio vectorial es de 2^n, en otras palabras, esta representación tiene complejidad es exponencial en espacio.

    En este documento, exploramos otra forma de representación basada en la composición de programas —deterministas— generadores de secuencias-f.

    Un programa generador toma —generalmente— como entrada una secuencia-f y da como salida otra secuencia-f. Si se considera que estas operaciones son deterministas, entonces la representación de secuencias se puede basar en la composición de programas y —por convención— la secuencia que representa al Código de Gray.

    El documento está disponible en el archivo pgfs.pdf.

    Repositorios:

  • image

    Reporte técnico de “Búsqueda de secuencias-f mínimas”

    En este trabajo presentamos un algoritmo de búsqueda de secuencias-f mínimas que representan familias de ciclos hamiltonianos en un hipercubo y un algoritmo de decisión de minimalidad en prefijos de secuencias-f.

    Mostramos el procedimiento de búsqueda de secuencia-f mínimas tomando como entrada un entero positivo, n, que representa la dimensión del hipercubo.

    Este algoritmo funciona con dos ideas principales: (1) la búsqueda en profundidad de los valores válidos para cada elemento de la secuencia, y (2) la identificación de segmentos de secuencia que son prefijos mínimos.

    El documento está disponible en el archivo schminfs.pdf.

    Repositorios: