La clase PNMatrix

Esta clase es el objeto principal de la red de Petri, pues mantiene los identificadores de los objetos gráficos que conforman la red de Petri. Aprovechando las características que ofrece la matriz de incidencia para representar a una red de Petri de una manera sencilla y compacta (ver 2.5.2 y 3.2 ), se eligió manejar internamente a las redes de Petri como un objeto que trabaja como una matriz de incidencia, manteniendo en su primer renglón (renglón 0) identificadores a los objetos Transition, en la primera columna (columna 0) identidicadores a los objetos Place, y en las intersecciones de los renglones y columnas a los objetos arcos que únen a los lugares con las transiciones, 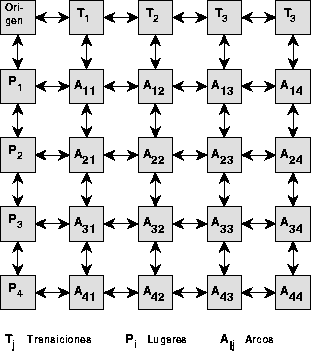como se puede apreciar en la figura 4.3.

  

Figure 4.3: Los objetos de la clase PNMatrix, representan a una red de Petri, como una matriz de incidencia

La ventaja que representa manejar a una red de Petri de esta forma, sobre las tradicionales (lista de elementos, y matriz de conectividad, ver figura 4.4), es que la forma de matriz de incidencia es más compacta y mantiene toda la información necesaria de la red e Petri, por ejemplo: si se trabajara con las listas ligadas se deberían implantar mecanismos para conocer la funciones de entrada y salida, y con la matriz de conectividad se tendría el problema del espacio en memoria. Por otro lado la forma de matriz de incidencia permite que se pueda pensar a futuro en una implantación de redes jerárquicas.

  

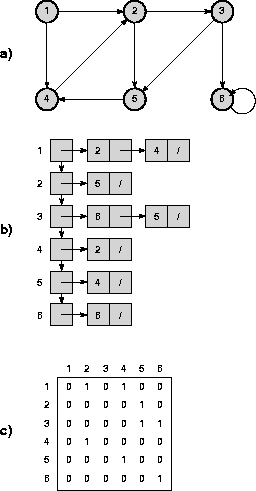
Figure 4.4: Representaciones tradicionales de un grafo dirigido

Además la matriz de incidencia permite a los objetos Place y Transition, conocer cuales son los arcos con los que están conectados y obtener información de estos para determinar, por ejemplo, cuales son los lugares de entrada y salida en una transición.

Si trabajamos con un enfoque de matriz de incidencia (figura  4.3) de elementos gráficos obtenemos:

• Los objetos Place se almacenan el la primera columna de la matriz (teniendo una lista ligada entre los diferentes lugares).

• Los objetos Transition se almacenan en el primer renglón de la matriz (teniendo una lista ligada entre las diferentes transiciones).

• Los objetos Connection se encuentran en los elementos que forman la intersección entre columnas (Transitions) y renglones (places).

Para implantar la clase PNMatrix se pensó en tener una clase padre que manejará a una matriz (la clase Matrix) y a la clase PNMatrix como una subclase que manejara específicamente tareas propias de la matriz de incidencia, como agregar transiciones, lugares, o enviar un mensaje a todo los objetos Transition, por mencionar algunos.

Las variables y métodos de instancia de la clase PNMatrix son:

@interface PNMatrix : Matrix
{
   int nPlaces;	    //Numero de lugares
   int nTransitions;//Numero de transiciones
   int nLinks;      //Numero de ligas
}
- (void)addPlace: (id)newPlace;
- (void)addTransition: (id)newTransition;
- (void)deletePlaceInRow: (int)i;
- (void)deleteTransitionInColumn: (int)j;
- (result_add)addConnection: (id)newConnection;
- (id)placeCanResponseToEvent:(NSEvent *)theEvent;
- (id)transitionCanResponseToEvent:(NSEvent *)theEvent;
- (id)graphCanResponseToEvent:(NSEvent *)theEvent;
- (void)reDrawAllConnectionsInColumn: (int)j;
- (void)reDrawAllConnectionsInRow: (int)i;
- (void)runTransitions;

Las variables nPlaces, nTransitions y nLinks se utilizan para mantener un control sobre, como sus nombres lo indican, el número de lugares, renglones y conexiones, respectivamente.

Los métodos de instancia de los objetos PNMatrix. Los mesajes son enviados a estos objetos por los objetos PNView.

addPlace

Este mensaje le llega al objeto por parte de un objeto PNView. Cuando se recibe este mensaje se agrega una nueva columna a la matriz y se hace referencia el objeto Place que se manda como parámetro de entrada en la primera columna del nuevo rengón.

addTransition

Cuando se recibe este mensaje se agrega un nuevo rengón a la matriz y se hace referencia el objeto Transition que se manda como parámetro de entrada en el primer rengón de la nueva columna.

deletePlaceInRow

Cuando se recibe este mensaje se borra el renglón especificado, lo que resulta en la eliminación de lugar y de todos sus arcos de entrada y salida.

deleteTransitionInColumn

Cuando se recibe este mensaje se borra la columna especificado, lo que resulta en la eliminación de la transición y de todos sus arcos de entrada y salida.

addConnection

Cuando se recibe este mensaje, se verifica la existencia de una referencia en la intersección de la transición y el lugar que contiene el objeto Connection que se manda como parámetro de entrada. Si no existe ninguna referencia, entonces se procede a hacer la referencia y se termina el trabajo. Si existe alguna referencia, entonces se verifica si el objeto existente mantiene la misma dirección que el nuevo objeto Connection, de ser así, entonces se aumenta el valor del peso del arco en el objeto existente. Si la dirección es contraria entre el objeto existente y el nuevo objeto Connection, entonces se disminuye el valor del peso del arco en el objeto existente. Si este peso llega a cero, entonces se procede a eliminar al objeto Connection existente.

placeCanResponseToEvent

Se recorre la primera columna de la matriz, y a los objetos Place se les envía el mensaje canResponseToEvent.

transitionCanResponseToEvent

Se recorre el primer rengón de la matriz y a los objetos Transition se les envía el mensaje canResponseToEvent.

graphCanResponseToEvent

Cuando se recibe este mensaje, el objeto PNMatrix manda los mensajes placeCanResponseToEvent y canResponseToEvent.

reDrawAllConnectionsInColumn

Cuando se recibe este mensaje, se recorre toda la columna, indicada en el parámetro de entrada, y si hay objetos Connection se les envía el mensaje reDraw.

reDrawAllConnectionsInRow

Cuando se recibe este mensaje, se recorre todo el rengón, indicado en el parámetro de entrada, y si hay objetos Connection se les envía el mensaje reDraw.

runTransitions

Cuando se recibe este mensaje, se recorre el primer rengón de la matriz y a los objetos Transition se les envía el mensaje run.