Técnicas de reducción o descomposición

Una estrategia para facilitar el análisis, es reducir el sistema a un modelo más simple el cual pueda conservar sus propiedades de análisis. Las técnicas para transformar un modelo abstracto a un modelo más refinado, en una forma jerárquica, se pueden utilizar como síntesis.

Existen muchas técnicas de transformación para redes de Petri. No es difícil ver que las siguientes seis operaciones conservan las propiedades de acotamiento, seguridad y activación [2].

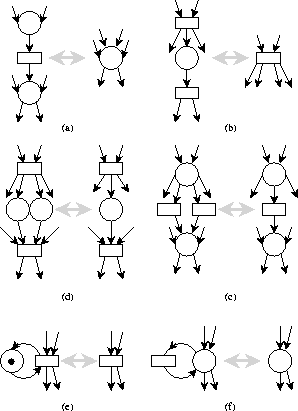
La figura 2.6 muestra distintas transformaciones que conservan propiedades de análisis según la especificación en cada caso.

a Fusión de una serie de lugares.

b Fusión de una serie de transiciones.

c Fusión de lugares paralelos.

d Fusión de transisiones paralelas.

e Eliminación de auto-ciclos de lugares.

f Eliminación de auto-ciclos de transiciones

  

Figure 2.6: Transformaciones que conservan propiedades de análisis