


Next: Técnicas de reducción o
Up: Ecuación de estado
Previous: Ecuación de estado
Suponga que una marca destino Md se alcanza desde una marca M0
a través de una secuencia de disparos
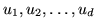 .
Escribiendo la ecuación de estado (2.1) para
.
Escribiendo la ecuación de estado (2.1) para
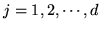 y sumándolos tenemos el siguiente desarrollo:
y sumándolos tenemos el siguiente desarrollo:
| M1 |
= |
M0 + ATu1 |
|
| M2 |
= |
M1 + ATu2 = M0 + ATu1 + ATu2 |
|
| M3 |
= |
M2 + ATu3 = M0 + ATu1 + ATu2 + ATu3 |
|
| |
 |
|
|
| Md |
= |
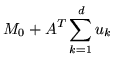 |
(2.2) |
La ecuación 2.2 puede escribirse como:
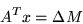 |
(2.3) |
donde
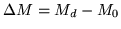 y
y
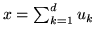 .
El vector columna x de dimensión
.
El vector columna x de dimensión 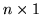 ,
con entradas de
enteros no negativos, se denimona vector de conteo de disparos. La
i-ésima entrada de x denota el número de veces que la
transición i se debe disparar para transformar M0 en Md.
Además de [25] se tiene que el conjunto de ecuaciones
algebraicas lineales 2.3 tiene una solución x, sí
y solo sí,
,
con entradas de
enteros no negativos, se denimona vector de conteo de disparos. La
i-ésima entrada de x denota el número de veces que la
transición i se debe disparar para transformar M0 en Md.
Además de [25] se tiene que el conjunto de ecuaciones
algebraicas lineales 2.3 tiene una solución x, sí
y solo sí, 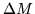 es ortogonal a cada solución y de este
sistema homogeneo:
es ortogonal a cada solución y de este
sistema homogeneo:
Sean r el rango de A, y la siguiente partición de A
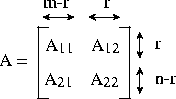
donde A12 es una matriz cuadrada no singular de orden
r. Un conjunto de (m-n) soluciones linealmente independientes
y para 2.4 se puede dar como los (m-r) renglones de
la siguiente matriz Bf de
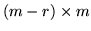 elementos
elementos
donde 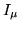 es la matriz identidad de orden
es la matriz identidad de orden 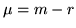 .
Note
que ABfT=0, lo que quiere decir es que el espacio vectorial obtenido
por los vectores renglón de A es ortogonal al espacio vectorial
obtenido por los vectores renglón de Bf. La matriz Bf corresponde
a la matriz de circuito fundamental para el caso de grafos
marcados[20]. Ahora, la condición de que
.
Note
que ABfT=0, lo que quiere decir es que el espacio vectorial obtenido
por los vectores renglón de A es ortogonal al espacio vectorial
obtenido por los vectores renglón de Bf. La matriz Bf corresponde
a la matriz de circuito fundamental para el caso de grafos
marcados[20]. Ahora, la condición de que 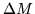 sea ortogonal a cada solución para Ay=0 es equivalente a la
siguiente condición:
sea ortogonal a cada solución para Ay=0 es equivalente a la
siguiente condición:
Así, si Md es alcanzable desde M0, entonces el vector
correspondiente x de conteo de disparos, debe existir y ser válido.



Next: Técnicas de reducción o
Up: Ecuación de estado
Previous: Ecuación de estado
Amilcar Meneses
2002-11-08
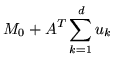
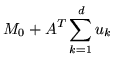

![]() elementos
elementos