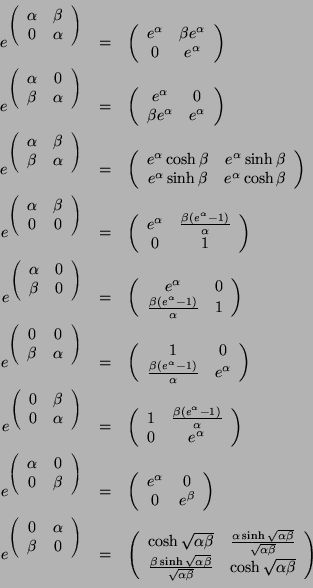Tabla de e^A.

Referencia rápida de algunos resultados de e^A, donde A es una matriz $n\times n$:

Definición: Sea A una matriz $n\times n$, entonces, la función e^A se define como

$$e^A = \mathrm{1}+ \sum_{n=1}^{\infty} \frac{A^n}{n!}$$

Donde 1 denota a la matriz unitaria de $n\times n$.

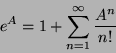
Note que si A y B son matrices $2\times 2$, entonces e^A+B = e^B+A, sólo si A y B conmutan, es decir si AB=BA.

Podemos ver, entonces, los siguientes resultados:

$$\begin{eqnarray*}e^0 & = & \mathrm{1}\\ e^{\mathrm{1}} & = & % \left(\begin{arr... ...y}{cc} \cosh 1 & \sinh 1 \\ \sinh 1 & \cosh 1 \end{array}\right) \end{eqnarray*}$$

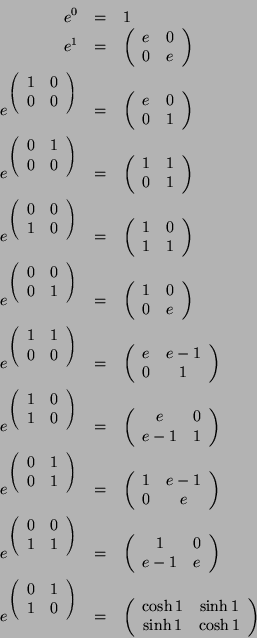
Ahora veamos los casos generales, sean $\alpha\in\mathbb{C}$.

$$\begin{eqnarray*}e^{\left(\begin{array}{cc} \alpha & 0 \\ 0 & 0 \end{array}\righ... ...a & \sinh\alpha \\ \sinh\alpha & \cosh\alpha \end{array}\right) \end{eqnarray*}$$

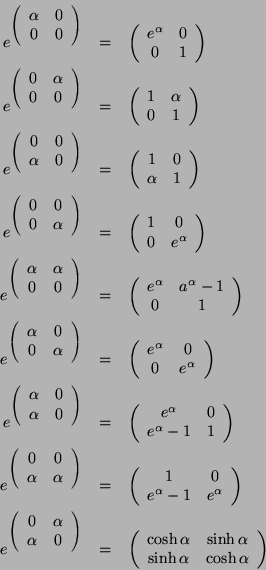
Sea $\alpha, \beta\in\mathbb{C}$, entonces:

$$\begin{eqnarray*}e^{\left(\begin{array}{cc} \alpha & \beta \\ 0 & \alpha \end{ar... ...t{\alpha\beta}} & \cosh\sqrt{\alpha\beta} \end{array}\right) \\ \end{eqnarray*}$$