Encargado: Dr. Matias Alvarado
ocuate@computacion.cs.cinvestav.mx
Resumen, dibujo y tema musical relacionado a mi investigación:https://t.co/WzGLiEUcjX
— Oliver Cuate (@CuateOliver) September 6, 2019
Herramientas de Exploración para el Tratamiento de Problemas de Optimización con Muchos Objetivos
Mi tema de investigación se relaciona con la toma de decisiones en el contexto de la optimización con muchos objetivos, es decir, problemas en los que se requiere optimizar de manera simultánea más de tres funciones objetivo. En particular, la idea es obtener un conjunto pequeño de soluciones, basadas en las preferencias de un tomador de decisiones, las cuales se expresan en forma de direcciones para explorar tanto el espacio de las variables como su imagen, el espacio de los objetivos.
Un primer enfoque fue propuesto en mi tesis de maestría, pero se limitaba a trabajar con problemas continuos y doblemente diferenciables, además de presentar algunas otras limitaciones, que fueron tratadas a lo largo de mi invetigación en el doctorado. Por ejemplo, ahora no es necesario que los problemas sean diferenciables, o bien, podemos tratar con problemas que solo lo son una vez, como los problemas lineales
Otro aspecto que se perfeccionó es la elección de un conjunto inicial de buenas soluciones, a partir de las cuales el tomador de decisiones pueda comenzar a explorar.
Además, tratamos con el problema olvidado de dar diversidad en el espacio de las variables, ya que la mayoría de los algoritmos se basan solo en mejorar los objetivos.
Por último, para probar nuestros métodos, fue necesario proponer un cojunto de funciones de prueba con restricciones de igualdad (que no existía en la literatura), así como tratar con una aplicación del mundo real. En este caso fue el proceso de inyección de plástico, con el que obtuvimos buenos resultados.
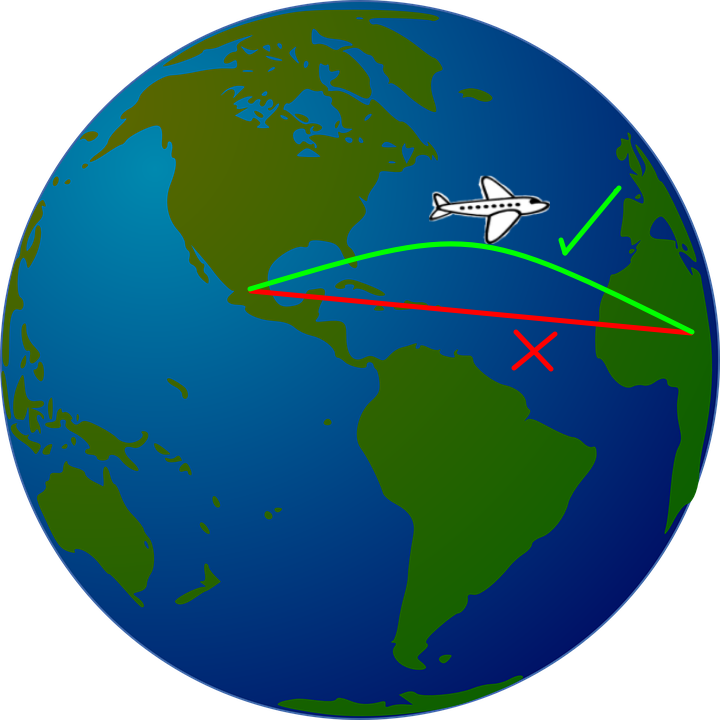
Mi dibujo muestra dos rutas posibles para un vuelo. La ruta más corta en esta geometría no es la aparente línea recta, sino que es aquella con una curvatura en su ruta. Esa curva es lo que se conoce como trayectoria ortodrómica. Esto se relaciona con mi investigación ya que se trata de seguir una dirección, que representa las preferencias del tomador de decisiones. Al igual que con las ruras aéreas, la forma de hacer esto sin perder optimalidad no es simplemente seguir tal cual dicha dirección.

El tema que escogí en la clase fue Sentado de Mariana Vega. La razón es que yo relaciono la letra con el proceso de investigación, en el que uno se puede equivocar y será criticado, pero es mejor intentar que quedarse sentado sin hacer nada nuevo.
Un tema más adecuado sin duda es Blue Jeans and Bloody Tears, una de las canciones que han sido creadas por una Inteligencia Artificial. La relación con mi tema de investigación es directa, ya que una de las herramientas que más he utilizado son los algoritmos evolutivos.
Con respecto a las matemáticas, incluyo un tema de Till Lindemann, vocalista de uno de mis grupos favoritos, Rammstein. La canción se llama Mathematik y menciona varios términos matemáticos, aunque no con la mejor intención.
Por último (a reserva de que esta lista siga creciendo) incluyo una interpretación en piano de la sucesión de números de Fibonacci.
Los archivos originales de esta actividad pueden descargarse aqui.