


Next: Matriz de incidencia y
Up: Métodos de Análisis
Previous: Métodos de Análisis
Dada una red de Petri (N,M0) desde una marca inicial M0 podemos
obtener tantas nuevas marcas como transiciones habilitadas. Así, de
cada nueva marca podemos obtener más marcas. Este proceso genera un
árbol de marcas. Los nodos representan las marcas generadas a partir de
M0 (la raíz) y sus sucesores, y cada arco representa un disparo
de una transición, la cual transforma una marca en otra.
Algunas de las propiedades que se pueden estudiar utilizando el árbol de
alcanzabilidad T para una red de Petri (N,M0) son las siguientes:
- 1.
- Una red (N,M0) es acotada y así R(N,M0) es finito
si y solo si
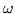 no aparece en nigún nodo etiquetado en T.
no aparece en nigún nodo etiquetado en T.
- 2.
- Una red (N,M0) es libre si y solo si solo aparecen ceros y unos
en las etiquetas de los nodos de T.
- 3.
- Una transición t es muerta si y solo si no aparece como etiqueta
de un arco en T.
- 4.
- Si M es alcanzable desde M0, entonces existe un nodo etiquetado
M' tal que
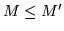 .
.



Next: Matriz de incidencia y
Up: Métodos de Análisis
Previous: Métodos de Análisis
Amilcar Meneses
2002-11-08