Next: Acotamiento
Up: Propiedades de comportamiento
Previous: Propiedades de comportamiento
La alcanzabilidad es una base fundamental para estudiar las propiedades
dinámicas de cualquier sistema. El disparo de una transición
habilitada cambiará la distribución de los tokens en una red, de
acuerdo a las reglas de transición mencionadas en la definición 3.
Una secuencia de disparos dará como resultado una secuencia de marcas.
Se dice que una marca 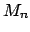 es alcanzable de una marca
es alcanzable de una marca 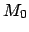 si existe
una secuencia de disparos que transformen a
si existe
una secuencia de disparos que transformen a 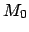 en
en 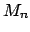 . Un secuencia
de disparos se denota por
. Un secuencia
de disparos se denota por
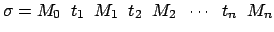 o simplemente por
o simplemente por
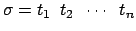 En este caso
En este caso 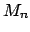 es alcanzable por
es alcanzable por 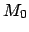 y se denota como
y se denota como
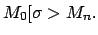 El conjunto de todas las marcas posibles alcanzables por
El conjunto de todas las marcas posibles alcanzables por 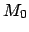 en una
red
en una
red 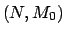 se denota como
se denota como 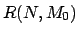 . El conjunto de todas las
secuencias de disparo desde
. El conjunto de todas las
secuencias de disparo desde 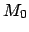 en una red
en una red 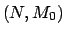 se denota como
se denota como
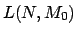 .
.
El problema de alcanzabilidad en las redes de Petri consiste en encontrar una
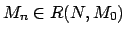 deseada.
deseada.
PetrA
ameneses@computacion.cs.cinvestav.mx /
amilcar@synge.stp.dias.ie
![]() deseada.
deseada.