Next: Ecuación de estado
Up: Matriz de incidencia y
Previous: Matriz de incidencia y
Para una red de Petri pura4 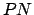 con
con 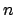 transiciones y
transiciones y 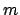 lugares, la matriz de
incidencia
lugares, la matriz de
incidencia ![$A=[a_{ij}]$](img67.png) es una matriz
es una matriz 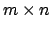 de enteros y su
entrada esta definida por:
de enteros y su
entrada esta definida por:
donde
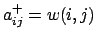 es el peso del arco de la transición
es el peso del arco de la transición 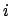 a
su lugar de salida
a
su lugar de salida 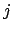 , y
, y
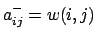 es el peso del arco de
la transición
es el peso del arco de
la transición 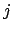 a su lugar de entrada
a su lugar de entrada 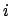 . Esto es, la matriz de
incidencia representa los lugares de entrada con valores negativos, y
los valores positivos representan salidas. Además una transición
. Esto es, la matriz de
incidencia representa los lugares de entrada con valores negativos, y
los valores positivos representan salidas. Además una transición
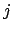 se encuentra habilitada en una marca
se encuentra habilitada en una marca 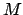 si
si
Para hacer pura a una red de Petri se deben sustituir los autociclos
por ciclos, como se muestra en la figura [5]
Figure:5
Transformación de autociclos a ciclos
|
|
PetrA
ameneses@computacion.cs.cinvestav.mx /
amilcar@synge.stp.dias.ie