Next: Persistencia
Up: Propiedades de comportamiento
Previous: Reversibilidad y estado inicial
Se dice que una marca 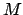 en una red de Petri
en una red de Petri 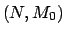 se puede cubrir
si existe una marca
se puede cubrir
si existe una marca
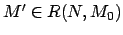 tal que
tal que
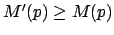 para cada
para cada
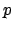 en la red. La propiedad de cubrir está muy relacionada con la
propiedad
en la red. La propiedad de cubrir está muy relacionada con la
propiedad 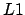 -activa de las transiciones. Sea
-activa de las transiciones. Sea 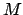 la marca mínima
para habilitar la transición
la marca mínima
para habilitar la transición 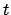 . Entonces
. Entonces 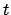 está muerto sí
y solo sí,
está muerto sí
y solo sí, 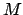 no se puede cubrir. El corolario a lo anterior nos
dice que si
no se puede cubrir. El corolario a lo anterior nos
dice que si 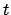 es
es 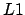 -activa sí y solo sí,
-activa sí y solo sí, 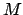 sepuede cubrir.
sepuede cubrir.
PetrA
ameneses@computacion.cs.cinvestav.mx /
amilcar@synge.stp.dias.ie